A large amount of the content for this section has been covered in 1.2.2 – Secondary storage. This is because it is essential you understand what data actually is before you learn about how it can be stored in large quantities (and what those quantities are). This information is repeated below for ease of access. However, there is new information here in the first section “Why data must be converted.”
In this section (click to jump)
Why data must be converted
As discussed in the very first topic – 1.1.1 – The Architecture of the CPU, you will have by now discovered that computers are binary devices. This means they absolutely cannot, under any circumstances, process or understand anything which is not data in the form of a one or a zero. No exceptions.
To summarize, a computer has the following properties:
- It is an electronic device
- Electricity can be controlled by either turning the current on or off
- The current being on represents a one (1) and off represents a zero (0)
- This switching of the current on or off is controlled by tiny switches called transistors
- Transistors may be connected in such a way that they create circuits capable of applying logical rules that are the foundation of all computer instructions
Hopefully you can see why a computer uses the binary number system – it is the only choice we have when the building blocks of computers are on/off switches.
There is a classic exam question that we can now answer:
Explain why computers require data in binary form [2]
Answer: Computers are devices made up of switches called transistors. These have only two states – on (1) and off (0), therefore all data must be in this format for a computer to process it.
This GCSE goes into great detail about how certain types of data are converted in to this binary form and it is all covered in Unit 1.2.4 – Data Conversion. It is much better to read that section in detail than to generalize here. However, we can state with authority the following:
Any data or information which is sent in (input) to a computer system must first be converted into binary. Any data or information the computer outputs, whether on a display, via sound, lights flashing, printing or any other method must first be converted from binary into this other form.
See Unit 1.2.4 for details on how images, sound and text are converted to and from binary.
Storage Quantities (The units of data storage)
We know that storage is a non-volatile place where we store 1’s and 0’s without losing them when the power is turned off. Now we need to turn our attention to how we measure the quantity of binary data that each device can store.
You’ll have heard the terms Gigabyte and Megabyte (especially when it comes to your mobile phone data allowance or contracts) but what do these actually mean?
If we take a detour for a moment and look around, you will see measurement systems are in use everywhere. How far was it to school this morning? 5km? How tall are you? 176cm? How much does a bus weigh? 5000Kg?
Focusing on one of those systems, weight, every single one of you will know the following:
The smallest unit of weight we usually use is the gram. 1g of something is not a lot at all, for example the average spoon full of sugar will weigh approximately 15g.
What if we have a lot of something? It would be silly to write “The weight of an average car is 23029201 grams.” Instead we write “2.3 tons” There is obviously a scale being applied here:
- 1 unit = 1 gram
- 1000 grams = 1 Kilogram (Kg)
- 1000 Kg = 1 Ton
- 1000 Tons = 1 Kiloton
- 1000 Kilotons = 1 Megaton
- 1000 Megatons = 1 Gigaton
Take notice of the words that are used here – Kilo, Mega and Giga as these are common to different measurement systems and we make use of them in computing to measure quantities of data.
Let’s get back to computing storage quantities.
First of all the smallest quantity we can store in a computer us a single zero or one:
- a 0 or a 1 = a Bit
Then we start grouping many bits together to make bigger quantities:
- 4 bits = a Nybble (no I didn’t make it up.)
- 8 bits = a Byte
- 1024 Bytes = 1 Kilobyte (Kb)
- 1024 Kilobytes = 1 Megabyte (Mb)
- 1024 Megabytes = 1 Gigabyte (Gb)
- 1024 Gigabytes = 1 Terabyte (Tb)
It shouldn’t be too hard to spot the pattern and this is what makes it easy to remember. As soon as you know 8 bits = a byte, then every quantity after that is 1024 of the previous amount.
That would be too easy if we just left it there, wouldn’t it?
Have you asked yourself why we are using multiples of 1024? The answer is because these storage quantities are powers of 2 (2 because we are using a binary number system). Why does this matter?
It matters because somewhere in the not so distant past, the computing community decided to redefine these storage quantities to be powers of 10, or multiples of 1000 rather than 1024. This makes it easier to perform calculations in your exam and harder for anyone to follow what on earth is going on.
The following table from IBM shows what we are talking about:
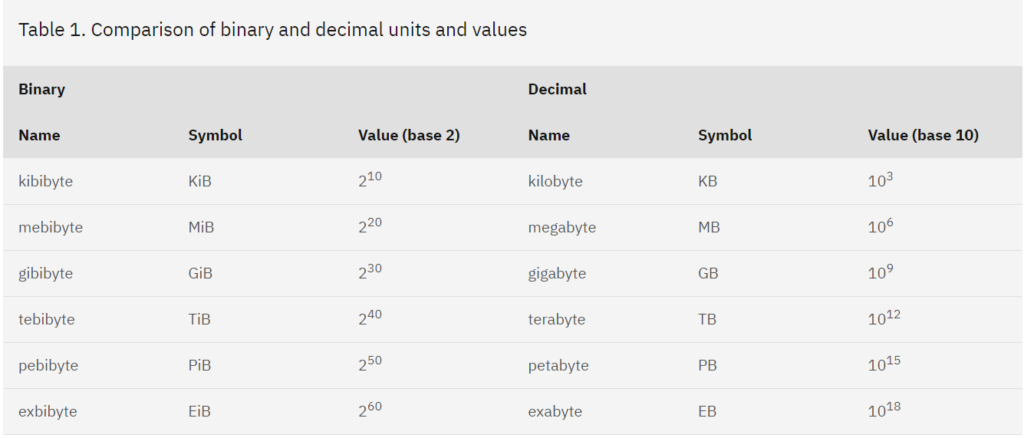
Notice that the names have swapped. A Gigabyte now is 1000 megabytes. The “old” terms now have different names. How confusing.
Our “new” table now looks something like this:
- 4 bits = a Nybble (no I didn’t make it up.)
- 8 bits = a Byte
- 1000 Bytes = 1 Kilobyte (Kb)
- 1000 Kilobytes = 1 Megabyte (Mb)
- 1000 Megabytes = 1 Gigabyte (Gb)
- 1000 Gigabytes = 1 Terabyte (Tb)
Please note, no one in the exam is going to be pedantic enough to mark you down or wrong for mixing up “megabyte” and “mebibyte” for example, so just use the words above interchangeably whether you are using powers of 10 or powers of 2. It doesn’t matter.
My advice on this is as follows:
- In the exam, use multiples of 1000
- Computers, regardless of what anyone else is doing, will always measure storage using powers of 2, and therefore the “old” multiples of 1024.
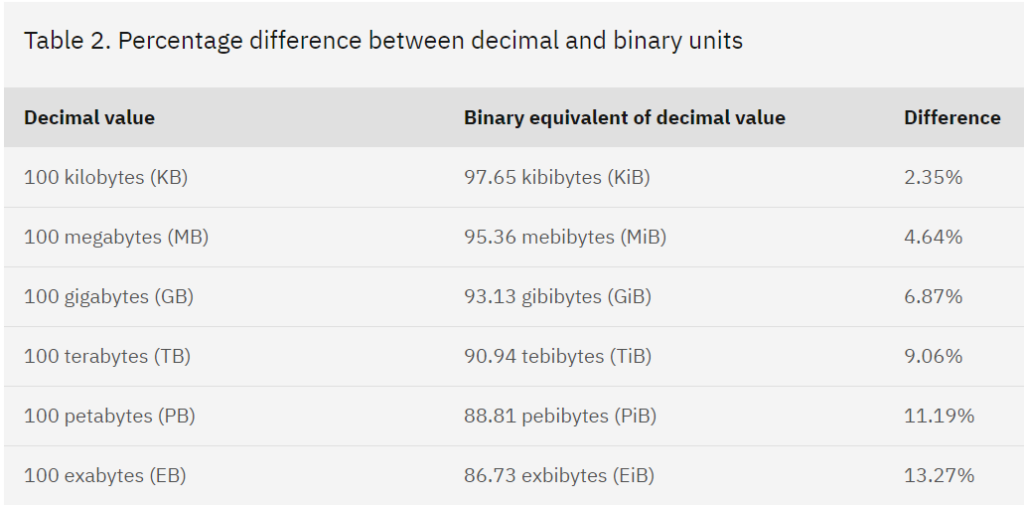
- This explains why when you buy a “1tb” SSD for your PS5, it sees it as being around 900Gb. It is using a different storage scale!
The scale of this storage loss can be seen in the table (also by IBM) provided below:
Calculating and converting storage requirements
When OCR changed the specification for the computing exam, they decided you need to be able to convert between the different storage quantities and also to calculate how much storage space would be required in a given scenario.
Examples of questions might be:
“How many gigabytes are in 2 terabytes?”
“A storage device has 2gb free space, how many 300mb videos could fit in the available space?”
Conversions and Calculations
You are likely to be asked to perform simple conversions between the different binary storage quantities. Below is a typical question from the November 2020 Unit 1 exam paper:

The question gives you two key pieces of information:
- There are 80 gigabytes of space available
- Files are 200,000 kilobytes in size
To answer any of these questions, you must know your storage quantities inside out. Lets repeat our table from earlier as a reminder:
- 8 bits = a Byte
- 1000 Bytes = 1 Kilobyte (Kb)
- 1000 Kilobytes = 1 Megabyte (Mb)
- 1000 Megabytes = 1 Gigabyte (Gb)
- 1000 Gigabytes = 1 Terabyte (Tb)
To answer this question we need to convert one of the quantities so that the units match – in other words, we need to be working with gigabytes and gigabytes.
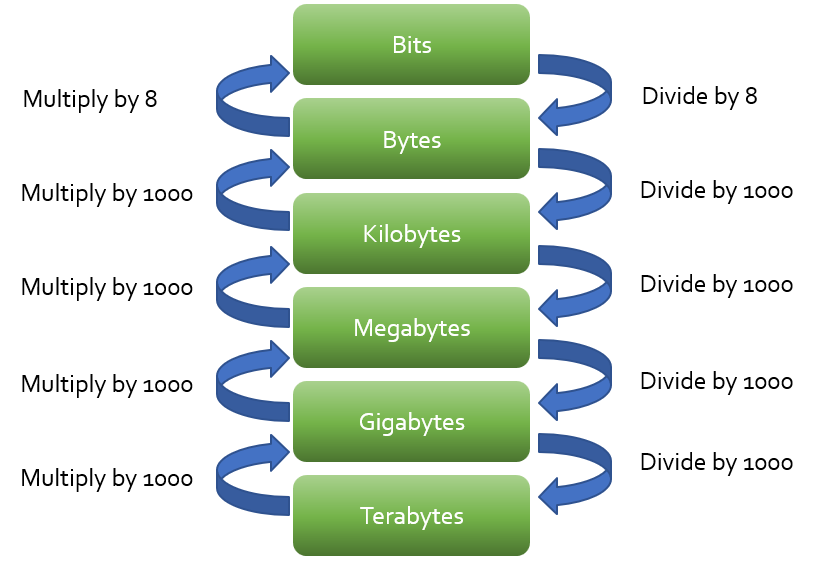
Conversions are really easy if you can remember the order in which these units go. To convert “up” the scale, from bytes to kilobytes to megabytes and so forth, simply divide by 1000. To convert “down” the scale, from megabytes to kilobytes to bytes and so forth, simply multiply by 1000. The diagram below illustrates this:

Going back to our question, how many 200,000 Kilobyte files can fit into 80 Gigabytes?
- 200,000 Kilobytes / 1000 = 200 Megabytes
- 200 Megabytes / 1000 = 0.2 Gigabytes
- 80 Gigabytes / 0.2 Gigabytes = 400 files
Alternatively you could do:
- 200,000 Kb / 1000 = 200 Megabytes
- There are 1000 Megabytes in a Gigabyte, therefore 1 Gigabyte can store 5 files (1000/200)
- 80 Gigabytes * 5 files per Gigabyte = 400 files
