
This section of the specification has the potential to be very large as it covers four distinct topics. I’ve split it up into those four sections, so this is 1.2.4 – Data Storage Part 1 – Numbers. That’s nice and clear isn’t it?
In this section we focus solely on the three number systems we need to understand:
- Decimal (or denary as they call it in the exam)
- Binary (you’ve met this before)
- Hexadecimal
The rules which govern these number systems are, thankfully, identical so once you understand one of them, you should be able to cope with all of them.
In this page (click to jump):
How digits, numbers and number systems work
Can you count to 10? If you can, you’re actually doing something quite complicated without realising and you’re also using all of the rules which define how all number systems work.
What on earth am I on about?
We should all agree that there are a lot of numbers – hence the word infinite, there are a never ending amount of numbers. How do we write down any number you could ever imagine? Do we come up with a special symbol for each new number? Of course not, we apply a simple set of rules which means that any number can be made up from a small set of digits. These rules are called a number system.
What is a number system?
A number system defines:
- How many digits there are
- What those digits are
- The value of each column of digits
Using these three rules we can make any number imaginable.
Let’s break this down using the number system you have been familiar with your whole life – Decimal.
The word Decimal comes from the numeric prefix “Dec” which means “of ten.” There are ten digits in the decimal number system:

A digit is a single symbol, that cannot be broken down further, used to represent a number. Digits may be combined in any order to create bigger numbers based on their place.
| Example | which is a… |
| 7 | Digit |
| 9 | Digit |
| 87 | Number, two digits combined |
| 965 | Number, three digits combined |
But why, for example, is the digit 6 worth six on its own yet represents 60 if I place another digit after it?
The answer is that all number systems have a rule that:
The value of a digit depends on its place in a number, the column that it is in.
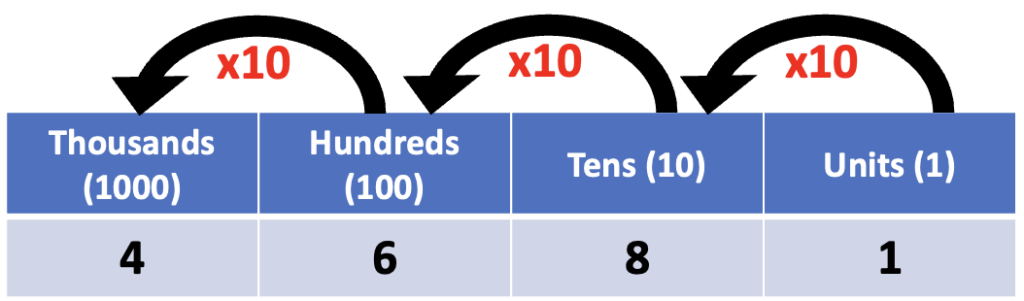
| Thousands | Hundreds | Tens | Units |
| 4 | 6 | 8 | 1 |
You can see that the number above is made up of only digits – 4, 6, 8 and 1. Their values depend on which column they are in. Therefore, the number above is actually:
4 x 1000
6 x 100
8 x 10
1 x 1
We would never normally think like this! But this concept is absolutely key to how a number system works. If you can understand the following, you’ll be fine:
- All numbers are made up from a small set of digits
- We can combine those digits to make any number
- The value of a digit is determined by the column it is in
- To work out the digit value, simply multiply the digit by the column value
Finally, there is one more question to ask – where do the values of these columns come from?
The answer is quite simple, we have ten digits and therefore each column is worth ten times more than the previous. This rule “number of digits X previous column value” applies to all number systems.
Moving to a binary number system
Decimal, as we know, has ten digits. Binary, coming from the prefix Bi meaning “of two” has only two digits.

Surely we can’t make any number by just using two digits, can we? Well, let’s apply the same rules as we learned before.
Firstly, apply the rule about column values. In decimal, each column was worth 10x the previous column because we had ten digits. We don’t have ten digits in Binary, we have two. Therefore, each column is worth 2x the previous column value, as shown below:
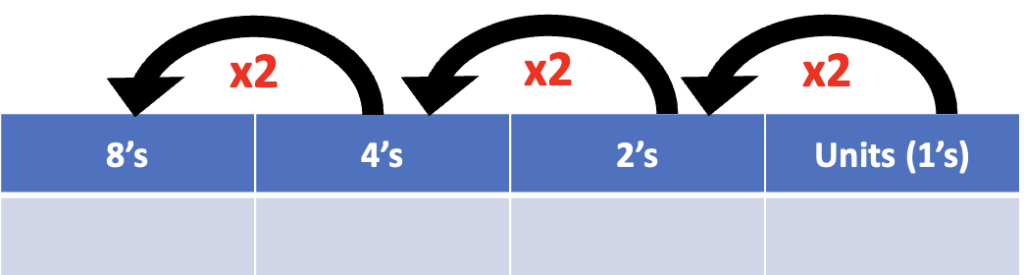
Binary numbers work in exactly the same way as decimal numbers – simply take the digit in each column and multiply it by the column value:

The number above is:
8 X 1 = 8
4 X 0 = 0
2 X 1 = 2
1 X 1 = 1
8 + 2 + 1 = 11
Binary is actually much simpler than it first appears. You will know that any number multiplied by zero is… zero! So, in Binary, whenever you see a zero, simply ignore it.
It gets better – any number multiplied by 1 is itself. Therefore, when you see a binary number you only need to do two things:
- Write out the column values
- Wherever there is a 1, add that column value to a running total
Another example is below, see if you can work out what number this is:

The videos below explain the binary number system in detail.
Decimal
Binary
Hexadecimal
Hexadecimal is a number system that exists solely to make our lives easier when dealing with large numbers in computing. Instead of two or ten digits, hexadecimal has 16 digits and because we don’t have symbols for digits above 9 we use the letters A to F as digit symbols.
This sounds wildly complicated, but it actually isn’t – certainly not when you’ve understood the rules of number systems and you can convert numbers in to, and from, binary.
Hexadecimal has some really nice properties for computer scientists:
- One single hexadecimal digit represents four binary digits
- Hexadecimal makes binary numbers far shorter
- We are less likely to make mistakes when reading and communicating hexadecimal numbers than binary numbers
It is important to remember that computers cannot understand hexadecimal – never forget that a computer is a binary only device, we use systems like hexadecimal only to make data more friendly for humans to read.
Watch the video below for all the detail you need about hexadecimal.
